
Lý thuyết về vị trí tương đối của hai đường tròn
1. Các kiến thức cần nhớ
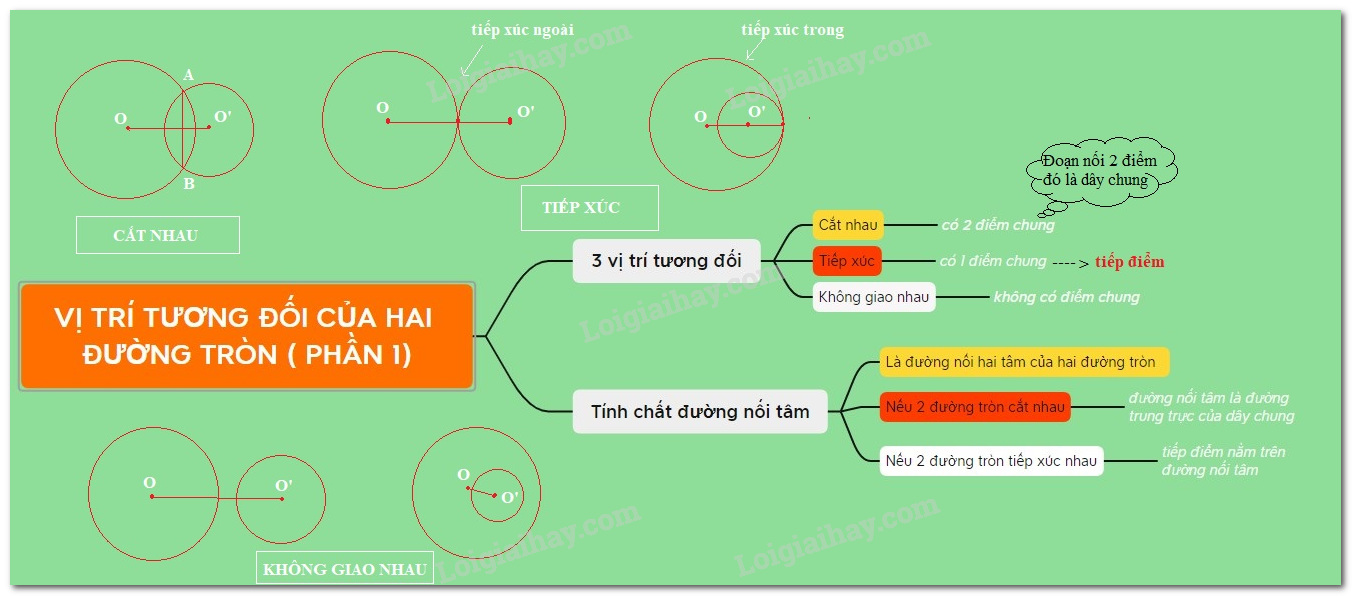
Trường hợp 1: Hai đường tròn $left( {O;R} right)$ và $left( {O';r} right)$ với $left( {R > r} right)$ cắt nhau
Khi đó $left( O right)$ và $left( {O'} right)$ có hai điểm chung và đường nối tâm là đường trung trực của đoạn $AB$.
Hệ thức liên hệ $R - r < OO' < R + r$
Trường hợp 2: Hai đường tròn tiếp xúc
+) Hai đường tròn $left( {O;R} right)$ và $left( {O';r} right)$ với $left( {R > r} right)$ tiếp xúc trong tại $A$.
Khi đó $A$ nằm trên đường nối tâm và $OO' = R - r$.
+) Hai đường tròn $left( {O;R} right)$ và $left( {O';r} right)$ với $left( {R > r} right)$ tiếp xúc ngoài tại $A$.
Khi đó $A$ nằm trên đường nối tâm và $OO' = R + r$.
Trường hợp 3: Hai đường tròn không giao nhau
+) Hai đường tròn $left( {O;R} right)$ và $left( {O';r} right)$$left( {R > r} right)$ ở ngoài nhau.
Ta có $OO' > R + r$
+) Hai đường tròn đựng nhau
Ta có $OO' < R - r$
+) Hai đường tròn đồng tâm
Ta có $OO' = 0$.
Ta có bảng sau
Vị trí tương đối của hai đường tròn $left( {O;R} right)$ và $left( {O';r} right)$ với $R > r$
Số
điểm chung
Hệ thức giữa $d$ và $R,r$
Hai đường tròn cắt nhau
$2$
$R-r < d < R + r$
Hai đường tròn tiếp xúc nhau
$1$
- Tiếp xúc ngoài
$d = R + r$
- Tiếp xúc trong
$d = R-r$
Hai đường tròn không giao nhau
$0$
-Ở ngoài nhau
$d > R + r$
- $left( O right)$ đựng (left( {O'} right))
$d < R - r$
- $left( O right)$ và (left( {O'} right)) đồng tâm
$d = 0$
Đường nối tâm là trục đối xứng của hình tạo bởi hai đường tròn. Từ đó suy ra :
- Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
- Nếu hai đường tròn cắt nhau thì đường nối tâm là đường trung trực của dây chung.
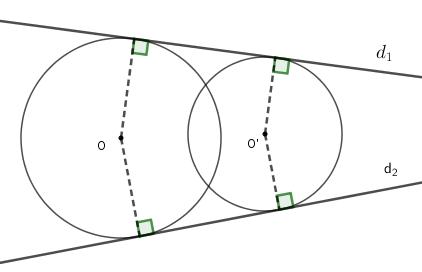
c. Tiếp tuyến chung của hai đường tròn
Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
Ví dụ: Hai đường tròn (O) và (O') cắt nhau thì có hai tiếp tuyến chung là hai đường thẳng $d_1$ và $d_2$ (hình vẽ)
2. Các dạng toán thường gặp
Dạng 1: Các bài toán có hai đường tròn tiếp xúc với nhau
Phương pháp:
Sử dụng tính chất hai đường tròn tiếp xúc:
+ Tiếp điểm nằm trên đường nối tâm
+) Hệ thức (d = R + r)
Khi làm có thể vẽ tiếp tuyến chung của hai đường tròn (nếu cần)
Dạng 2: Các bài toán có hai đường tròn cắt nhau
Phương pháp:
Nối dây chung của hai đường tròn rồi dùng tính chất đường nối tâm của hai đường tròn
Hệ thức liên hệ : $R-r < d < R + r$
Dạng 3: Các bài toán tính độ dài, diện tích
Phương pháp:
Sử dụng tính chất đường nối tâm, tính chất tiếp tuyến.
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông.
Link nội dung: https://world-link.edu.vn/duong-thang-tiep-xuc-voi-duong-tron-a65588.html