Mời thầy cô và các bạn tham khảo Bộ 12 đề thi học kì 1 Toán 7 sách Kết nối tri thức năm học 2023 - 2024 do VnDoc đăng tải sau đây. Đề thi Toán 7 học kì 1 năm 2023 được biên soạn bám sát nội dung học trong SGK Kết nối tri thức. Đây không chỉ là tài liệu hay cho các em ôn luyện trước kỳ thi mà còn là tài liệu cho thầy cô tham khảo ra đề. Sau đây mời các bạn tham khảo chi tiết.
Lưu ý: Toàn bộ 12 đề và đáp án đều có trong file tải về. Mời các bạn tải về xem trọn bộ tài liệu
1. Đề thi Toán 7 học kì 1 Kết nối tri thức - Đề 1
(Bộ đề thi có sử dụng đề của GiaiToan.com. VnDoc được phép khai thác độc quyền tài liệu này!)
I. Phần trắc nghiệm (4 điểm)
Câu 1: Viết phân số (frac{{25}}{{99}}) dưới dạng số thập phân:
A. (0,25)
B. 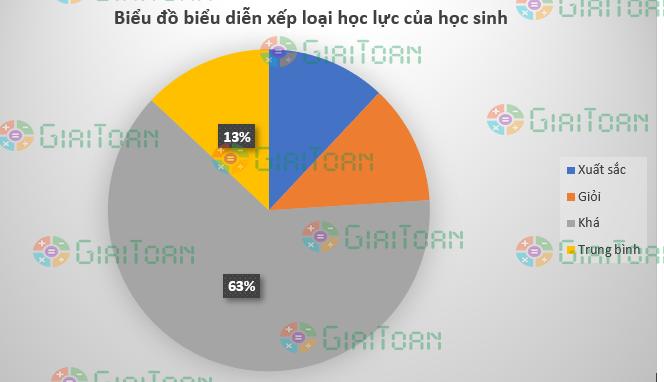 (0,2left( 5 right))
(0,2left( 5 right))
C. (0,left( {25} right))
D. (0,left( {025} right.))
Câu 2: Kết quả làm tròn số 0,7125 đến chữ số thập phân thứ 3 là:
A. (0,712)
B. (0,71)
C. (0,710)
D. (0,713)
Câu 3: Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau:
Tìm tỉ số phần trăm số học sinh xuất sắc của lớp đó. Biết rằng số học sinh xuất sắc bằng số học sinh giỏi.
A. 24%
B. 12%
C. 10%
D. 15%
Câu 4: Chọn câu trả lời đúng: Nếu a là một số vô tỉ thì:
A. a cũng là một số tự nhiên
B. a cũng là một số nguyên
C. a là một số hữu tỉ
D. a là một số thực
Câu 5: Giá trị của biểu thức (A = frac{{sqrt {16} }}{2} + frac{{sqrt {25} }}{5} + frac{{sqrt {100} }}{{10}} - frac{{50}}{3})
A. 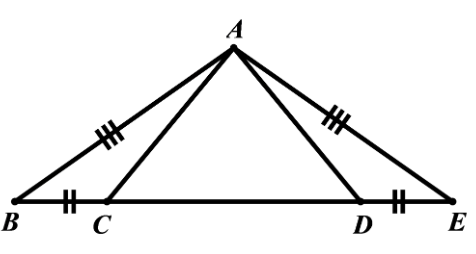 (A = frac{{38}}{3})
(A = frac{{38}}{3})
B. (A = - frac{{38}}{3})
C. (A = frac{{62}}{3})
D. (A = - frac{{46}}{3})
Câu 6: Sắp xếp các số sau theo thứ tự từ nhỏ đến lớn: (sqrt 5 ;2;pi ;frac{{13}}{4}; - sqrt {10} ;10)
A. (- sqrt {10} ;sqrt 5 ;2;pi ;frac{{13}}{4};10)
B. (- sqrt {10} ;2;sqrt 5 ;frac{{13}}{4};pi ;10)
C. (- sqrt {10} ;2;sqrt 5 ;pi ;frac{{13}}{4};10)
D. (- sqrt {10} ;2;pi ;sqrt 5 ;frac{{13}}{4};1)
Câu 7: Số hữu tỉ x thỏa mãn ({left( {2x - 1} right)^3} = frac{8}{{125}})
A. (x = frac{{ - 7}}{{10}})
B. (x = frac{{ - 3}}{{10}})
C. (x = frac{3}{{10}})
D. (x = frac{7}{{10}})
Câu 8: Cho tam giác ABC cân tại A, phân giác trong của góc A cắt cạnh BC tại D. Khẳng định nào sau đây sai?
A. Đường thẳng AD là đường trung trực của cạnh BC
B. (Delta ADB = Delta ADC)
C. (Delta ADB = Delta ADC)
D. (widehat {ABC} + widehat {ADC} = {180^0})
Câu 9: Cho hình vẽ:
Biết a // b, (widehat {{A_1}} - widehat {{B_1}} = {50^0}). Tính số đo góc (widehat {{B_1}})?
A. (widehat {{B_1}} = {130^0})
B. (widehat {{B_1}} = {75^0})
C. (widehat {{B_1}} = {65^0})
D. (widehat {{B_1}} = {50^0})
Câu 10: Cho đoạn thẳng AB có độ dài 6cm. Đường trung trực d của B cắt AB tại M. Mệnh đề nào sau đây sai?
A. MA = MB = 6cm
B. MA = MB = 3cm
C. M là trung điểm của AB
D. d vuông góc với đường thẳng AB
II. Phần tự luận (6 điểm)
Câu 1: Thực hiện các phép tính:
a) (A = left( {frac{1}{3} - frac{1}{5}} right):frac{5}{3} - left( {frac{5}{3} - frac{1}{5}} right):frac{5}{3})
b) (B = 2 + frac{1}{{1 + dfrac{1}{2}}})
c) (C = frac{{sqrt {{{left( { - 5} right)}^2}} }}{1} + frac{{sqrt 9 }}{{15}} - frac{{sqrt {81} }}{2} + frac{{sqrt {{{left( { - 8} right)}^2}} }}{{10}})
d) (D = sqrt {frac{{11}}{{25}} + 1} - sqrt {20} left( {frac{1}{{sqrt {80} }} - frac{1}{{3sqrt {10} }}} right) + frac{1}{6})
Câu 2: Tìm x biết:
a) (2 + frac{{19}}{5}:left( {3x} right) = frac{{11}}{3})
b) (x.left( {x + frac{{11}}{4}} right) = 0)
c) (frac{{x + 2}}{{3 - x}} = frac{3}{7};left( {x ne 3} right))
Câu 3: Cho tam giác ABC có các góc đều nhọn, AB < AC. Tia phân giác của góc A cắt cạnh BC tại D. Vẽ BE vuông góc với AD tại E. Tia BE cắt cạnh AC tại F.
a) Chứng minh AB = AF
b) Qua F vẽ đường thẳng song song với BC, cắt AE tại H. Lấy điểm K nằm giữa D và C sao cho FH = DK. Chứng minh DH = KF và DH // FK.
c) Chứng minh widehat {ACB}' width='109' height='23'>(widehat {ABC} > widehat {ACB})
Câu 4: Tính tổng A = x + y + z, biết
(frac{{19}}{{x + y}} + frac{{19}}{{y + z}} + frac{{19}}{{z + x}} = frac{{7x}}{{y + z}} + frac{{7y}}{{z + x}} + frac{{7z}}{{x + y}} = frac{{133}}{{10}})
Đáp án đề thi học kì 1 môn toán lớp 7 KNTT
I. Phần trắc nghiệm (4 điểm)
II. Phần tự luận (6 điểm)
Câu 1:
a) (A = - frac{4}{5})
b) (B = frac{8}{3})
c) (C = frac{3}{2})
d) (D = frac{{13 + 5sqrt 2 }}{{15}})
2. Đề thi Toán 7 học kì 1 Kết nối tri thức - Đề 2
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Trong các câu sau, câu nào đúng?
A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;
B. Số 0 là số hữu tỉ dương;
C.Số nguyên âm không phải là số hữu tỉ âm;
D. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm.
Câu 2. Trong các số sau, số nào biểu diễn số đối của số hữu tỉ -0,5?
A. 1/2;
B. −1/2;
C. 2;
D. -2.
Câu 3. Số (-frac{1}{3}) là số:
A. Số thập phân vô hạn không tuần hoàn;
B. Số thập phân hữu hạn;
C. Số thập phân vô hạn tuần hoàn;
D. Số vô tỉ.
Câu 4. (sqrt{64}) bằng:
A. ± 8;
B. -8;
C. 8;
D. 64.
Câu 5. Nếu |x| = 2 thì:
A. x = 2;
B. x = -2;
C. x = 2 hoặc x = -2;
D. Không có giá trị nào của x thỏa mãn.
Câu 6. Quan sát hình vẽ.
Có tất cả bao nhiêu góc kề bù với (hat{NGC})?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 7. Trong các câu sau, câu nào không phải định lí?
A. Nếu hai góc bằng nhau thì chúng đối đỉnh;
B. Nếu hai góc kề bù thì tổng số đo của chúng bằng 180°;
C. Nếu hai góc bù nhau thì tổng số đo của chúng bằng 180°;
D. Nếu hai góc đối đỉnh thì chúng bằng nhau.
Câu 8. Tổng số đo ba góc của một tam giác là
A. 45°;
B. 60°;
C. 90°;
D. 180°.
Câu 9. Phát biểu nào dưới đây là sai?
A. Hai tam giác có các góc tương ứng bằng nhau là hai tam giác bằng nhau;
B. Hai tam giác bằng nhau thì có các góc tương ứng bằng nhau;
C. Hai tam giác có các góc tương ứng bằng nhau, các cạnh tương ứng bằng nhau thì hai tam giác đó bằng nhau.
D. Hai tam giác bằng nhau là hai tam giác có các cạnh bằng nhau và có các góc bằng nhau.
Câu 10. Cho các hình vẽ sau:
Hình vẽ nào minh họa đường thẳng d là đường trung trực của đoạn thẳng AB?
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Câu 11. Thân nhiệt (°C) của bạn An trong cùng khung giờ 7h sáng các ngày trong tuần được ghi lại trong bảng sau:
Bạn An đã thu được dữ liệu trên bằng cách nào?
A. Xem tivi;
B. Lập bảng hỏi;
C. Ghi chép số liệu thống kê hằng ngày;
D. Thu thập từ các nguồn có sẵn như: sách, báo, web.
Câu 12. Kết quả tìm hiểu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C cho bởi bảng thống kê sau:
Kết quả tìm hiểu về khả năng chơi bóng đá của các bạn học sinh nữ của lớp 7C được cho bởi bảng thống kê sau:
Khẳng định nào dưới đây là đúng?
A. Dữ liệu về khả năng chơi cầu lông của các bạn học sinh nam lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;
B. Dữ liệu về khả năng chơi bóng đá của các bạn học sinh nữ lớp 7C đại diện cho khả năng chơi cầu lông học sinh cả lớp 7C;
C. Dữ liệu về khả năng chơi cầu lông và bóng đá được thống kê chưa đủ đại diện cho khả năng chơi thể thao của các bạn lớp 7C;
D. Lớp 7C có 35 học sinh.
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm )
Thực hiện phép tính:
a) (left( { - dfrac{3}{4} + dfrac{2}{3}} right):dfrac{5}{{11}} + left( { - dfrac{1}{4} + dfrac{1}{3}} right):dfrac{5}{{11}})
b) (dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}})
c) (left| {dfrac{3}{5} - dfrac{1}{{10}}} right| - sqrt {dfrac{{36}}{{25}}} + {left( {dfrac{3}{{10}}} right)^5}:{left( {dfrac{3}{{10}}} right)^4})
d) (sqrt {144} + sqrt {49} - 10sqrt {dfrac{4}{{25}}})
Bài 2: (2,0 điểm)
Tìm x, biết:
a) (left( { - dfrac{1}{2}} right) + left( {dfrac{4}{5} + x} right) = 1dfrac{1}{2})
b) ({left( {x - dfrac{1}{3}} right)^2} = dfrac{1}{9})
c) (5.sqrt x - sqrt {dfrac{1}{{25}}} = 0)
d) (left| {0,3 - x} right| = dfrac{1}{3})
Bài 3: (1,0 điểm)
Tính số đo của góc x trong hình vẽ dưới đây:
Bài 4: (1,5 điểm)
Cho tam giác ABC cân tại A có (widehat {A{rm{ }}} = 120^circ). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) (Delta BAM = Delta CAN);
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Bài 5: (0,5 điểm)
Tìm số thực x, biết: (left| x right| + left| {x + 2} right| = 0).
Đáp án Đề thi Toán 7 học kì 1 Kết nối tri thức - Đề 2
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
A
A
C
C
B
B
A
D
A
C
C
C
Phần II. Tự luận:
Bài 1
a) (left( { - dfrac{3}{4} + dfrac{2}{3}} right):dfrac{5}{{11}} + left( { - dfrac{1}{4} + dfrac{1}{3}} right):dfrac{5}{{11}})
(begin{array}{l} = left( { - dfrac{3}{4} + dfrac{2}{3}} right).dfrac{{11}}{5} + left( { - dfrac{1}{4} + dfrac{1}{3}} right).dfrac{{11}}{5} = left( { - dfrac{3}{4} + dfrac{2}{3} + dfrac{{ - 1}}{4} + dfrac{1}{3}} right).dfrac{{11}}{5} = left[ {left( { - dfrac{3}{4} + dfrac{{ - 1}}{4}} right) + left( {dfrac{2}{3} + dfrac{1}{3}} right)} right].dfrac{{11}}{5} = left( {dfrac{{ - 4}}{4} + dfrac{3}{3}} right).dfrac{{11}}{5} = left( { - 1 + 1} right).dfrac{{11}}{5} = 0.dfrac{{11}}{5} = 0end{array})
b)(dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}})
(begin{array}{l} = dfrac{{{{left( {{3^3}} right)}^{10}}.{{left( {{2^4}} right)}^{25}}}}{{{{left( {2.3} right)}^{30}}.{{left( {{2^5}} right)}^{15}}}} = dfrac{{{3^{3.10}}{{.2}^{4.25}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{5.15}}}} = dfrac{{{3^{30}}{{.2}^{100}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{75}}}} = dfrac{{{2^{100}}}}{{{2^{30 + 75}}}} = dfrac{{{2^{100}}}}{{{2^{105}}}} = dfrac{1}{{{2^5}}} = dfrac{1}{{32}}end{array})
c) (left| {dfrac{3}{5} - dfrac{1}{{10}}} right| - sqrt {dfrac{{36}}{{25}}} + {left( {dfrac{3}{{10}}} right)^5}:{left( {dfrac{3}{{10}}} right)^4})
(begin{array}{l} = left| {dfrac{6}{{10}} - dfrac{1}{{10}}} right| - dfrac{6}{5} + {left( {dfrac{3}{{10}}} right)^{5 - 4}} = left| {dfrac{5}{{10}}} right| - dfrac{6}{5} + {left( {dfrac{3}{{10}}} right)^1} = dfrac{5}{{10}} - dfrac{{12}}{{10}} + dfrac{3}{{10}} = dfrac{{ - 4}}{{10}} = dfrac{{ - 2}}{5}end{array})
d) (sqrt {144} + sqrt {49} - 10sqrt {dfrac{4}{{25}}})
(begin{array}{l} = 12 + 7 - 10.dfrac{2}{5} = 19 - 4 = 15end{array})
Bài 2
a) (left( { - dfrac{1}{2}} right) + left( {dfrac{4}{5} + x} right) = 1dfrac{1}{2})
(begin{array}{l} - dfrac{1}{2} + dfrac{4}{5} + x = dfrac{3}{2}x = dfrac{3}{2} - left( { - dfrac{1}{2}} right) - dfrac{4}{5}x = dfrac{3}{2} + dfrac{1}{2} - dfrac{4}{5}x = dfrac{4}{2} - dfrac{4}{5}x = 2 - dfrac{4}{5}x = dfrac{{10}}{5} - dfrac{4}{5}x = dfrac{6}{5}end{array})
Vậy (x = dfrac{6}{5})
b) ({left( {x - dfrac{1}{3}} right)^2} = dfrac{1}{9})
({left( {x - dfrac{1}{3}} right)^2} = {left( {dfrac{1}{3}} right)^2} = {left( { - dfrac{1}{3}} right)^2})
Trường hợp 1:
(begin{array}{l}x - dfrac{1}{3} = dfrac{1}{3}x = dfrac{1}{3} + dfrac{1}{3}x = dfrac{2}{3}end{array})
Trường hợp 2:
(begin{array}{l}x - dfrac{1}{3} = - dfrac{1}{3}x = dfrac{{ - 1}}{3} + dfrac{1}{3}x = 0end{array})
Vậy (x in left{ {dfrac{2}{3};0} right})
c) (5.sqrt x - sqrt {dfrac{1}{{25}}} = 0)
(begin{array}{l}5.sqrt x - dfrac{1}{5} = 05.sqrt x = dfrac{1}{5}sqrt x = dfrac{1}{5}:5 = dfrac{1}{5}.dfrac{1}{5} = dfrac{1}{{25}}end{array})
(begin{array}{l}sqrt x = sqrt {{{left( {dfrac{1}{{25}}} right)}^2}} Rightarrow x = dfrac{1}{{625}}end{array})
Vậy (x = dfrac{1}{{625}})
d) (left| {0,3 - x} right| = dfrac{1}{3})
(left| {dfrac{3}{{10}} - x} right| = dfrac{1}{3})
Trường hợp 1:
(begin{array}{l}dfrac{3}{{10}} - x = dfrac{1}{3}x = dfrac{3}{{10}} - dfrac{1}{3}x = dfrac{9}{{30}} - dfrac{{10}}{{30}}x = dfrac{{ - 1}}{{30}}end{array})
Vậy (x in left{ {dfrac{{ - 1}}{{30}};dfrac{{19}}{{30}}} right})
Trường hợp 2:
(begin{array}{l}dfrac{3}{{10}} - x = dfrac{{ - 1}}{3}x = dfrac{3}{{10}} - left( {dfrac{{ - 1}}{3}} right)x = dfrac{9}{{30}} + dfrac{{10}}{{30}}x = dfrac{{19}}{{30}}end{array})
Bài 3:
Xét (Delta ABC có: angle A + angle B + angle C = {180^0}) (định lý tổng ba góc trong một tam giác)
(begin{array}{l} Rightarrow {50^0} + x + {35^0} = {180^0} Rightarrow x + {85^0} = {180^0} Rightarrow x = {180^0} - {85^0} Rightarrow x = {95^0}end{array})
Vậy (x = {95^0})
Bài 4
a) Xét 2 tam giác vuông BAM và CAN có:
AB=AC (Do tam giác ABC cân tại A)
(widehat B = widehat C) (Do tam giác ABC cân tại A)
Delta BAM = Delta CAN(g.c.g)' width='239' height='22'>(=>Delta BAM = Delta CAN(g.c.g))
b)
Xét tam giác ABC cân tại A, có (widehat {A{rm{ }}} = 120^circ)có:
(widehat B = widehat C = frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}).
Xét tam giác ABM vuông tại A có:
(begin{array}{l}widehat B + widehat {BAM} + widehat {AMB} = {180^o} Rightarrow {30^o} + {90^o} + widehat {AMB} = {180^o} Rightarrow widehat {AMB} = {60^o} Rightarrow widehat {AMC} = {180^o} - widehat {AMB} = {180^o} - {60^o} = {120^o}end{array})
Xét tam giác MAC có:
(begin{array}{l}widehat {AMC} + widehat {MAC} + widehat C = {180^o} Rightarrow {120^o} + widehat {MAC} + {30^o} = {180^o} Rightarrow widehat {MAC} = {30^o} = widehat Cend{array})
(Rightarrow)Tam giác AMC cân tại M.
Vì BM=CN => BN=MC' width='405' height='17'>(Delta BAM = Delta CAN=>BM=CN => BN=MC)
Xét 2 tam giác ANB và AMC có:
AB=AC
(AN = AM(do Delta BAM = Delta CAN))
BN=MC
Delta ANB = Delta AMC(c.c.c)' width='237' height='22'>(=>Delta ANB = Delta AMC(c.c.c))
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Bài 5
Do (left| x right| ge 0;left| {x + 2} right| ge 0) với mọi số thực x nên (left| x right| + left| {x + 2} right| ge 0) với mọi số thực x.
Do đó, (left| x right| + left| {x + 2} right| = 0) khi (left| x right| = 0) và (left| {x + 2} right| = 0).
Suy ra x đồng thời bằng 0 và bằng - 2 (vô lí).
Vậy không có giá trị nào của x thỏa mãn yêu cầu của đề bài.
3. Đề thi Toán 7 học kì 1 Kết nối tri thức - Đề 3
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Số hữu tỉ là số viết được dưới dạng phân số a/b với:
A. a = 0, b ≠ 0;
B. a, b ∈ ℤ; b ≠ 0;
C. a, b ∈ ℕ;
D. a ∈ ℕ; ; b ≠ 0.
Câu 2: Trong các số sau, số nào viết được dưới dạng số thập phân vô hạn tuần hoàn?
A. 10
B. (frac{{15}}{3})
C. (frac{{ - 25}}{2})
D. (frac{8}{3})
Câu 3: Phát biểu nào dưới đây sai?
A. Số (frac{2}{7}) là một số vô tỉ
B. Số -2 là một số nguyên âm
C. Số 19 là một số tự nhiên
D. (sqrt 2) là một số vô tỉ
Câu 4. Căn bậc hai số học của số a không âm là:
A. √ a ;
B. − √ a ;
C. √ a và − √ a
D. Không có đáp án.
Câu 5. Nhận định nào sau đây là đúng?
A. 1,516 < 1,(516);
B. 1,516 = 1,(516);
C. 1,516 > 1,(516);
D. 1,516 ≈ 1,(516).
Câu 6: Tính số đo của góc x trong hình vẽ dưới đây:
A. x = ({85^0})
B. x = ({110^0})
C. x = ({115^0})
D. x = ({95^0})
Câu 7: Cho (Delta ABC = Delta DEF). Biết (angle A = {33^0}). Khi đó:
A. (angle D = {33^0})
B. (angle D = {42^0})
C. (angle E = {32^0})
D. (angle D = {66^0})
Câu 8: Số tam giác cân trong hình vẽ dưới đây là:
A. 2
B. 1
C. 4
D. 3
Câu 9: Đường trung trực của đoạn thẳng AB là đường thẳng …
A. song song với đoạn thẳng AB.
B. vuông góc với đoạn thẳng AB.
C. đi qua trung điểm của đoạn thẳng AB.
D. vuông góc với đoạn thẳng AB tại trung điểm của nó.
Câu 10. Điền vào chỗ chấm:
Đường thẳng … một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng ấy.
A. vuông góc với, một điểm;
B. cắt, một điểm;
C. cắt, trung điểm;
D. vuông góc với, trung điểm.
Câu 11. Dãy dữ liệu về cân nặng (đơn vị: kilôgam) của 7 học sinh lớp 7A: 25; 30; 32; 28; 29; 31; 27 thuộc loại dữ liệu nào?
A. Dữ liệu không là số;
B. Dữ liệu định tính;
C. Dữ liệu định lượng;
D. Dữ liệu kilôgam.
Câu 12. Thầy giáo muốn điều tra môn thể thao yêu thích của học sinh khối lớp 7 (gồm ba lớp 7A, 7B, 7C). Cách điều tra nào sau đây đảm bảo được tính đại diện?
A. Lấy ý kiến của các bạn nam;
B. Lấy ý kiến của các bạn nữ;
C. Lấy ý kiến của các bạn lớp 7A;
D. Lấy ý kiến ngẫu nhiên của các bạn trong cả ba lớp 7A, 7B, 7C.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm)
1. Thực hiện phép tính:
(a. 12-{{3}^{0}}:frac{1}{3}+{{left( frac{-1}{2} right)}^{2}})(b. 7frac{1}{2}+left( 2frac{1}{3}+3frac{1}{2} right):left( frac{-23}{6}+3frac{1}{7} right))2. Tìm x, biết:
(a. frac{x}{12}-frac{5}{6}=frac{1}{6})
b. (frac{2}{3}-1frac{4}{5}x=frac{-3}{5})
Bài 2. (3,0 điểm)
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho (widehat {CAM} = {30^o}). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
Bài 4. (1,0 điểm) Một nghiên cứu đã đưa ra tỉ lệ học sinh cấp THCS nghiện điện thoại di động trong những năm gần đây như biểu đồ sau:
a) Trục đứng biểu diễn đại lượng gì? Dữ liệu về đại lượng này thuộc loại nào?
b) Năm 2021, một trường THCS có 600 học sinh. Hãy ước lượng số học sinh nghiện điện thoại di động của trường THCS đó.
Bài 5. (1,0 điểm) Giá niêm yết của một chiếc điện thoại tại một cửa hàng vào tháng 10 là 12 000 000 đồng. Cứ sau một tháng thì giá của điện thoại lại giảm 5% so với giá bán niêm yết ở tháng trước. Sau hai tháng, cửa hàng bán chiếc điện thoại đó vẫn nhận được lãi 830 000 đồng so với giá nhập về. Hỏi giá nhập về của chiếc điện thoại này là bao nhiêu?
Đáp án đề thi Học kì 1 môn Toán lớp 7 Kết nối tri thức - Đề 2
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
B
D
A
A
A
D
A
A
D
C
C
D
PHẦN II. TỰ LUẬN (7,0 điểm)
Hướng dẫn giải phần tự luận
Bài 1.
Câu 1:
(a,12-{{3}^{0}}:frac{1}{3}+{{left( frac{-1}{2} right)}^{2}}=12-1.3+frac{1}{4}=9+frac{1}{4}=frac{37}{4})
(b,7frac{1}{2}+left( 2frac{1}{3}+3frac{1}{2} right):left( frac{-23}{6}+3frac{1}{7} right)=frac{15}{2}+left( frac{7}{3}+frac{7}{2} right):left( frac{-23}{6}+frac{22}{7} right)=frac{15}{2}+frac{35}{6}:frac{-29}{42}=frac{15}{2}-frac{245}{29}=frac{-55}{58})
Câu 2:
(a,frac{x}{12}-frac{5}{6}=frac{1}{6}Rightarrow frac{x}{12}=frac{1}{6}+frac{5}{6}Rightarrow frac{x}{12}=1Rightarrow x=12)
Vậy x = 12
(begin{align} & c,frac{2}{3}-1frac{4}{5}x=frac{-3}{5} & Rightarrow frac{2}{3}-frac{9}{5}x=frac{-3}{5} & Rightarrow frac{9}{5}x=frac{2}{3}+frac{3}{5} & Rightarrow frac{9}{5}x=frac{19}{15}Rightarrow x=frac{19}{27} end{align})
Vậy (x=frac{19}{27})
Bài 2.
a) Xét tam giác ABC có:
{90^o} + {60^o} + widehat C = {180^o} = > widehat C = {30^o}end{array}' width='214' height='83'>(begin{array}{l}widehat A + widehat B + widehat C = {180^o} = > {90^o} + {60^o} + widehat C = {180^o} = > widehat C = {30^o}end{array})
Xét tam giác CAM có (widehat A = widehat C = {30^o})
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
{30^o} + widehat {CMA} + {30^o} = {180^o} = > widehat {CMA} = {120^o} = > widehat {BMA} = {180^o} - widehat {CMA} = {180^o} - {120^o} = {60^o}end{array}' width='390' height='120'>(begin{array}{l}widehat C + widehat {CMA} + widehat {CAM} = {180^o} = > {30^o} + widehat {CMA} + {30^o} = {180^o} = > widehat {CMA} = {120^o} = > widehat {BMA} = {180^o} - widehat {CMA} = {180^o} - {120^o} = {60^o}end{array})
Xét tam giác ABM có:
{60^o} + {60^o} + widehat {BAM} = {180^o} = > widehat {BAM} = {60^o}end{array}' width='248' height='89'>(begin{array}{l}widehat B + widehat {BMA} + widehat {BAM} = {180^o} = > {60^o} + {60^o} + widehat {BAM} = {180^o} = > widehat {BAM} = {60^o}end{array})
Do(widehat {BAM} = widehat {BMA} = widehat {ABM} = {60^o}) nên tam giác ABM đều.
c) Do tam giác CAM cân tại M nên MA = MC (1).
Do tam giác BAM là tam giác đều MA = MB (2).
Từ (1) và (2) ta có MB = MC.
Mà M nằm giữa B và C nên M là trung điểm của BC.
Vậy M là trung điểm của BC.
Bài 3.
a) Trục đứng biểu diễn tỉ lệ học sinh THCS nghiện điện thoại di dộng. Dữ liệu này là dữ liệu số.
b) Quan sát biểu đồ ta thấy, tỉ lệ học sinh THCS nghiện điện thoại di dộng năm 2021 là 15%
Số học sinh của trường THCS đó nghiện điện thoại di dộng khoảng:
600 . 15% = 600 . 15/100 = 90 (học sinh).
Bài 4.
Giá bán của chiếc điện thoại ở tháng 11 là:
12 000 000 . (100% - 5%) = 11 400 000 (đồng).
Giá bán của chiếc điện thoại ở tháng 12 là:
11 400 000 . (100% - 5%) = 10 830 000 (đồng).
Sau hai tháng, cửa hàng vẫn lãi 830 000 đồng so với giá nhập về nên giá nhập về là:
10 830 000 - 830 000 = 10 000 000 (đồng).
Vậy giá nhập về của chiếc điện thoại này là 10 000 000 đồng.
Mời các bạn tải về xem toàn bộ 10 đề thi học kì 1 Toán 7 KNTT
..............................
Để chuẩn bị tốt cho kì thi học kì 1 lớp 7 sắp tới, các em học sinh cần thực hành luyện đề đề làm quen với nhiều dạng đề thi khác nhau và nắm được cấu trúc đề thi. VnDoc giới thiệu tới các bạn chuyên mục Đề thi học kì 1 lớp 7 với đầy đủ các môn. Đây là tài liệu hay cho thầy cô tham khảo ra đề, cũng là nguồn tài liệu để các em học sinh ôn luyện trước kì thi. Mời thầy cô và các em tham khảo.
Ngoài Top 11 đề thi học kì 1 Toán 7 Kết nối tri thức năm học 2023 - 2024, mời các bạn tham khảo thêm tài liệu học tập lớp 7 khác như Ngữ văn 7 , Toán 7 và các Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7 ... được cập nhật liên tục trên VnDoc.com.


